Pck Software

Technical details about Pck software

• The detection software is written in C++ using CGAL, the Computational Geometry Algorithms Library [CGAL06]
• The VMD-plugin is written in tcl and uses stooop, the Simple Tcl Only Object Oriented Programming package

Polyhedral model

Our models and algorithms relie on the alpha-shapes theory wich is briefly discribed in another section. As a summary, we consider atoms as spheres with their Van der Waals radii plus a constant probe radius. A molecule is thus depicted as a union of such spheres. We then inrtoduce a polyhedral model of the molecule where the vertices of the polyhedron are the centers of thoose atoms that have a part of their surface not completely engulfed by other spheres. The faces (triangles and edges) of this polyedron also depict intersections of atoms that occur freely outside all other atoms. This polyhedron is also often reffered as the dual-complex of the molecule and is desrcibed more formaly in another section.

Important remark : the dual-complex depicts exactly the molecular surface, but formaly it is not a representation of the molecule's surface. For instance it's vertices are not placed on the molecular surface, they are the centers of the molecule's atoms.

Fig.1 A polyhedral model : the dual complex

a.) A schematic two dimensional exemple : a pack of disks (2D-spheres) symbolize atoms, and it's dual shape 6 vertices, and edges and one triangle.	b.) A true molecular exemple, the dual shape of the main pocket of a VDR (1ie8.pdb)

Pck classification of facets in the polyhedral model

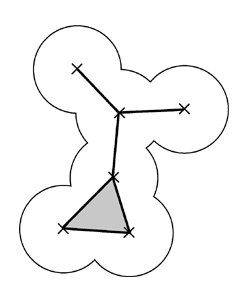
Remind that except for mouths, a facet in the polyhedral model indicates a blockage of the probe by the three atoms centered at the facet vertices. In our software we discriminate between five types of facets in the dual complex :

• regular facet (r) : Demarcates free space from the protein core.
• mouth facet (m) : Delimites the entrance the pocket space from the solvant space. A probe sphere can roll freely across this kind of facets.

Irregular facets reffer to the case where a probe sphere is blocked on both sides by the same three atoms.

• irregular pocket to infinity facet (p2i) : An "almost mouth" facet, it denote a place where the probe is blocked on one side in the pocket and on the other side in the solvant space.
• irregular pocket to other pocket facet (p2o) : Denote a place where the probe sphere is blocked in two distinct pockets by the same three atoms. Indicates a possible recruitement of a neighbouring pocket.
• irregular pocket to same pocket facet (p2p) : When three atoms block two times the probe sphere in the same pocket.

Pck pocket detection algorithms

Important remark : it is worth to insist on the fact that Pck seeks for pockets solely on geometric criteria. Thus, when we talk of pockets we should precise geometric pockets, as opposed to "ligand binding pockets" or "biological pockets". Nevertheless, as expressed in [REFS], biological pockets most often dwell in geometric pockets, thus a geometric definition of pockets might be a preliminary step for the study of biological pockets.

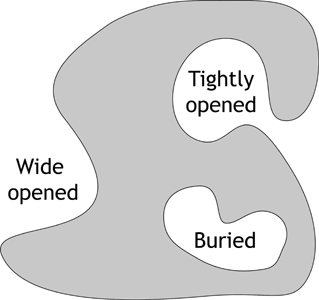
Pockets are usualy discriminated according to their shape : one talks of cavities for thoose voids that are totaly buried in the protein core, isolated from solvant space, of (closed) pockets for thoose that shrink in a narrow mouth before opening to the solvant; and of clefts for thoose that open wide to the solvant.

Fig.2 Different pockets shapes : Cavities are totaly buried, closed pockets have a narrow mouth, clefts are wide opened.

In our software the detection of pockets is achieved in the polyhedral model. We implemented two algorithms meant to detect different kind of pockets :

• tight : detects cavities and closed pockets. It is an implementation of Edelsbrunner's algorithm[Edel98] and relies on an alternative definition of closed pockets first given by kleinwegt[REF] : "closed pockets are those that would become cavities if we would fatten the atoms of the molecule ".
• wide : meant to detect clefts. Here pockets are defined as " the difference between two levels of details in the molecule's shape ". A definition was first given by masuya and doi[REF] as the difference between two molecular models using two different probe size, and an equivalent definition was then given in the polyhedral context by Peters[Peters96].

Pck convexity index

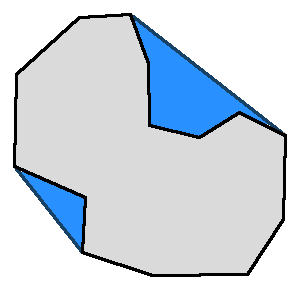
We define a convexity index for a pocket by comparing volumetric values of it's polyhedral model and of it's convex hull.

IndexV = 100 * V(ConvexHull) / V(Pocket)

This provides information on the "globularity" of the pocket. See (fig 3.a) for a 2D exemple.

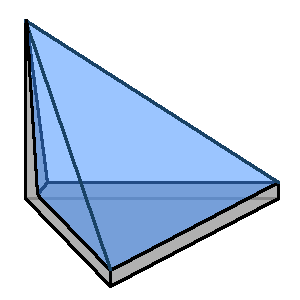
As a supplementary information we also provide the same information with regard to the surface instead of the volume. This information is to handle with care : The volume of a polyhedron is always smaller than the one of it's convex hull. As for the surface this is no longer the case. In 2D, the surface of an object is always greater or equal to the one of it's convex hull, which is not necessarily the case in 3D. Consider for instance a triangular flat box (Fig 3.b) with a long pin comming out from one of it's corners. The surface of the object will bee approximatively the surface of the box, whereas the surface of the convex hull will be approximatively the one of the tetrahedron composed of the corners of the box plus the one at the top of the pin.

Fig.3 A polyhedron and it's convex hull

a.) A 2D exemple of a pocket and of it's convex hull. The pocket is depicted by the grey polyedron, it'as convex hull is adds the blue parts to the pocket. The volume of the convex hull is bigger than the one of the pocket, it's surface is smaller. The more convex the pocket, the more it's volumetric convexity index tends to 1.	b.) An exemple that illustrates the fact that in 3D the surface of a polyhedron can be smaller than the one of it's convex hull. Here, the surface of the grey polyhedron is approximatively two time the one of it's basis triangle. The surface of the convex hull is approximatively twice.