Biology

Usual molecular models

In computational biology three models introduced during the 70's are commonly used for the representation of molecules :

• The Van der Waals model (VdW), where atoms are considered as spheres centered on their atomic center with their Van der Walls radius. The VdW surface of a molecule is the enveloppe of the union of it's VdW spheres (fig 1.a).
• The Accessible Surface (SA), also known as solvent excluded surface (SES) is a VdW-like model where the atoms radii are expended by a common constant reffered as the probe radius (fig 1.b). An equivalent definition considers a probe sphere freely rolling on the VdW surface of the molecule. The center of this rolling sphere delineates the SA.
• The Molecular Surface (MS) also known as Connolly Surface after the name of Michael Connolly who was the first to give an algorithm to construct it [Connolly86]. It is defined as the enveloppe of the space that the probe sphere cannot reach when it rolls around the VdW surface.

Fig.1 A two dimensional exemple of usual molecular models (the probe sphere is pictured red)

a.) VdW model	b.) SA model	c.) MS model

These three models usually find différent applications. The VdW model claims to represent the interracting surface of the molecule (from the point of view of most favorable VdW contacts). One usually preffers MS to VdW because it represents more accurately the space that can be accessible to a probe for a VdW contact and because it is smooth almost everywhere. As for the SA model, it more accurateely represents those places where a solvant probe sphere can be placed around the molecule; one of it's major uses is for the detection of pockets, since a pocket shall be a locus where at least a probe spere can stand.

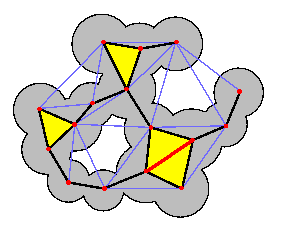
The dual shape, a polyedral model

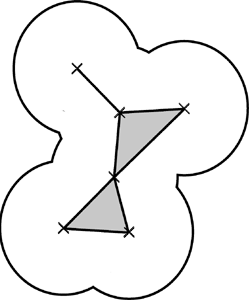
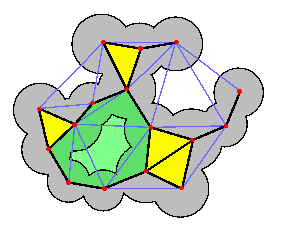
Although they give a good representation of a molecular surface, these three models are uneasy to comprehend at first sight, and therefore are not suitable for certain applications. The dual shape model (fig 2) introduced in 1995 is a polyedron and therefore gives a more human readable visualization of a molecule. The dual shape vertices are the centers of the atoms, it's edges link two atoms showing an intersection in the solvent space, it's triangles link three atom that have a common intersection in the solvent space. Because it is based on the atoms centers and because it exactly represents atoms intersections on the border of the molecule, this model no longer represents the molecular surface itself, but it depicts it very well.

Fig.2 A two dimensional exemple of the dual shape model, another molecular model
In 2D he dual shape of a pack of spheres is made of vertices, and edges. It's interior is composed of triangles, pictured gray here. In 3D it's made of interior is also made of vertices, edges and triangles; it's interior is made of tetrahedra.

a.) dual shape of the VdW model	b.) dual shape of the SA model

This model not only gives a better sight of a molecule's surface, but it also provides a combinatorial definition of the molecule that is far more suitable for a lot of computational jobs.

A more detailed description of this dual-shape model is given hereafter.

Alpha shapes

The alpha shape theory is a framework developped in the early 90's in computer science (more specifically in computational geometry) to address the problem of shape reconstruction from a set of points (that is "how to retrieve the shape of an object when we only have a sample of it's surface points ?"). Rapidely, it has been used for it's multi-level like description : alpha shape can as a matter of fact be seen as a hierarchical set of polyedron interpolating the sample point set with a lessening level of details.

Still Alpha shapes research developpements

Alpha-shapes

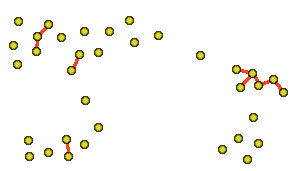
Alpha shapes are intimately linked with another computational geometry object : the Delaunay triangulation (see Fig.3 for an exemple in two dimensions) A triangulation consists in a partition of the 3D space in tetrahedra whose vertices are exactly the given point clouds. There are many ways to achieve this, but the Delaunay triangulation is the only one with the void sphere property (given a tetraedron in the Delaunay triangulation, the circumsphere of this tetrahedron does not host any other vertex of the point cloud). As a result, the Delaunay triangulation gives an intuitive and formal definition of points neighborhood : the neighbours of a point are thoose that are linked to this point by an edge in the Delaunay trianbglation.
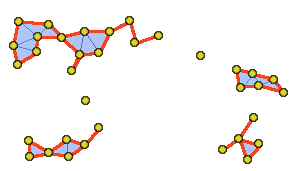
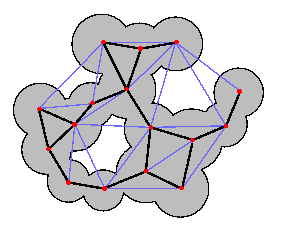
The alpha-shape is constructed on top of this triangulation. It consists of a collection of growing polyedron indexed by a finite number of alpha values. These polyedron are constructed by sorting the Delaunay simplices ("simplex" is a name to refer simultaneously to vertices, edges, triangles and tetraedra contained in the triangulation) on the basis of a "distance-like" critera. For instance, an edge in Delaunay trianglulation will enter the alpha shape when alpha is big enough according to the edge length.As illustrated in Fig.4, larger simplices will enter the alpha shape for bigger alpha values. In fact one can see the alpha parameter as the radius of some spheres that one would pin, centered on each points. An edge enters the alpha-shape when the spheres placed on the two corner vertices of the edge intersect.
To be exhaustive, there are two notions comming together : the alpha-complex refers to the set of all thoses simplices that are actually under the alpha threshold, whereas the alpha-shape is merely the border of this alpha-complex. As a shortcut both notions are usually reffered as "the alpha-shape". Moreover, the term "alpha-shape" is sometimes also used indifferently to refer to the whole collection of polyedron or to one of them for a fixed alpha value.

Fig.3 An exemple in 2D : a point set and it's Delaunay triangulation

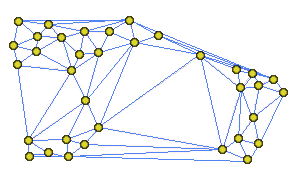A point cloud and	it's Delaunay triangulation

Fig.4 An exemple in 2D : Evolution of the alpha-shape and the alpha-complex as the alpha value grows. The simplices of the alpha-complex are pictured blue, those that also belong to the alpha-shape are pictured red.

For lower alpha values, the alpha-shape is nothing else but the point cloud	As alpha rises the smallest edges enter the alpha-shape and the alpha complex
As triangles enter the alpha complex, their linking edges leave the alpha-shape (blue edges were red for lower alpha values)
The alpha-shape and ythe alpha-complex goes on fattening untill the alpha-shape becomes the convex hull of the initial set of points. At this stage, the alpha-complex is the whole delaunay triangulation.

Ultimately, it is worth to say that there is a generalisation of alpha-shapes where one can modulate the importance given to points using a different weight for each of them. These "weighted points" can be seen as spheres, a vision that emphasize a natural bridge between weighted alpha-shapes [Edel92] and the most usual molecular models, as we'll see later.

Dual shape

As for the unweighted case, the construction of the alpha-shape in the weighted case starts with a Delaunay-like construction : the weighted Delaunay complex, also known as regular triangulation. Given a set of spheres, it's dual-shape and dual-complex are respectively the alpha-shape and the alpha-complex for an alpha value of 0.

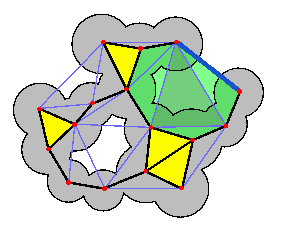
In 1995 delsbrunner exhibited [Edel95] a correspondance between these two constructions and the shape of the pack of sphere. In fact, the dual shape is the subset of Delaunay simplices (vertices, edges, triangles) whose composing spheres (thoose whose centers lie on the corners of the simplicex) present a common intersection at the surface of the union of spheres. One can see a to dimensional exemple in (fig.5 b).

Fig.5 A two dimensional exemple of the dual shape and the dual complex of a pack of spheres

a.) The dual shape of the pack of spheres is made of the bold black Delaunay edges. The others Delaunay edges are pictured in thin blue.	b.) The dual complex is the "interior" of the dual-shape, it adds the yellow triangles and the red edge to the dual shape.

(fig.6). summurizes the dual objects in the dual-shape and the union of spheres

As a shortcut one usually talks about "*the* alpha-shape" as a shortcut for the dual-shape or sometimes for the dual-complex.

Alpha shapes and biology

As previously stated, one common representation for molecules is the so called spacefililng model, that is to represent a molecule by a union of spheres (see VdW and SA models.). The early exhibition of the duality between dual-shapes and spacefilling models lead to their rapid use in structural biology.

Pocket detection

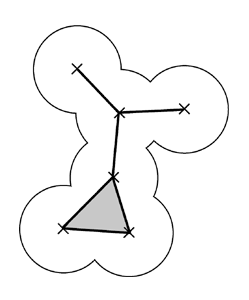
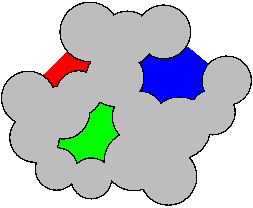
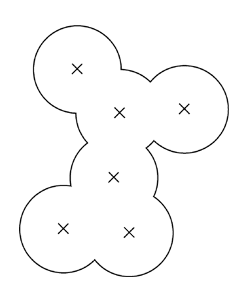
A natural first step in the detection of pockets is to give a definition of what we do call a "pocket". In (fig.7) one can see the three major kind of shapes one can intuitively discriminate.

Fig.7 The three major kind of "intuitive" pockets

In green : a cavitiy, which is totally buried inside the protein In blue : a (closed) pocket, which present a narrow mouth to the outside In red : a cleft, that is a wide opened pocket on the surface of the protein Clefts and pockets could surely be further classified on their shape, their number of mouths, the shape of their mouth,...

Then we must find formal definitions that coincides with this intuitions. The definition of internal cavities is clear enough. The definition of pockets can be reformulated in terms of growing spheres : "a pocket is a place that would become a cavity if I would grow the atoms". As a matter of fact, in the process of fattening atoms, the tiny gaps would shut before the big holes, thus isolating new cavities. As for clefts we'll define them as the difference between two level of details of a molecular surfaces.

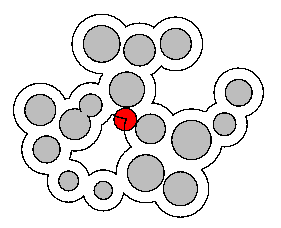
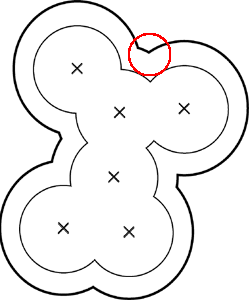
As expressed in (fig.8 a. and b.), the VdW model is really "porous", and not suitable for the detection of pockets. The SA model allows one to close these tiny gaps. Moreover, since a prerequisite of pockets is to contain something, it is natural to consider the use of this latest model when looking for pockets.

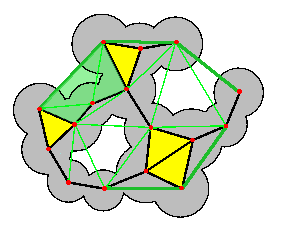
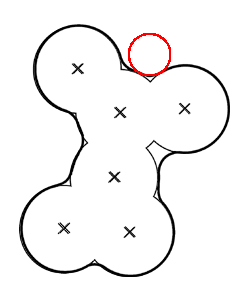
Detection of cavities is straightforward (fig.8 c) : cavities in the dual complex correspond to cavities in the molecule.

Detection of pockets is less immediate, we must first remark that in an alpha-complex there are special tetraedra (triangles in the 2D case) that do vanish (i.e. enter the alpha-complex in the process of growing alpha) after all their neighbors. These special tetraedra are called sinks and a all closed pockets must have at leat one of these sinks. So the detection of closed pockets (fig.8 d) is nothing more complicated than finding these sinks.

As for clefts, one can define them as the space that is trapped between two probes of different size (fig.8 e). In the alpha-shape context one can define them with the difference between two alpha-complexes. One generally choose the dual complex as a basis, and an alpha-complex for a positive alpha value as a bigger level of details.

Fig.8 Pocket detection with the dual shape

a.) Atoms in VdW model, represented by spheres. In three dimensions, the VdW is lacunary.	b.) The SA model reflect those places where a solvant can stand, it closes thoose annoying invaginations in the VdW model.
c.) A cavity (green triangles) in the dual-shape correspond to a cavitiy in the molecule	d.) A closed pocket in the dual shape that present one mouth (bold blue edge) and one sink (darker green triangle)
e.) An intuitive definition of a cleft	f.) And it's translation in the dual shape

In the context of pocket detection, alpha-shapes based methods present advantages on others methods : they allow pocket definitions that are both formal and combinatorial, these definitions agree with the intuitive ones, and finaly, nowadays they are the only methods that accuratly bound pockets, both answering the "can of worm" (lacunarity of the VdW model) and the "sea level" problems (where does the pocket end, and the solvant space begin).

Links

For more details on alpha shapes one can refer to the online biogeometry web site section dedicated to the alpha shapes.